※ 모바일 주의사항 ※
모바일 이용시 $ Latex수식 $이 적용되지 않는거 같습니다.
수식적용하는 script가 PC웹페이지에만 적용되는거 같습니다. 모바일은 쏴리..
상관계수
상관계수?
산점도에서 점들이 얼마나 직선에 가까운지를 타나내는 척도를 상관계수 라고 한다.
아래 그림을 보며 설명을 하자면, p의 값이 $ X_1 X_2$ 특징에 대해서 얼마나 직선적인 경향을 나타내는가를 수치로 수치로 표현한 것이다.
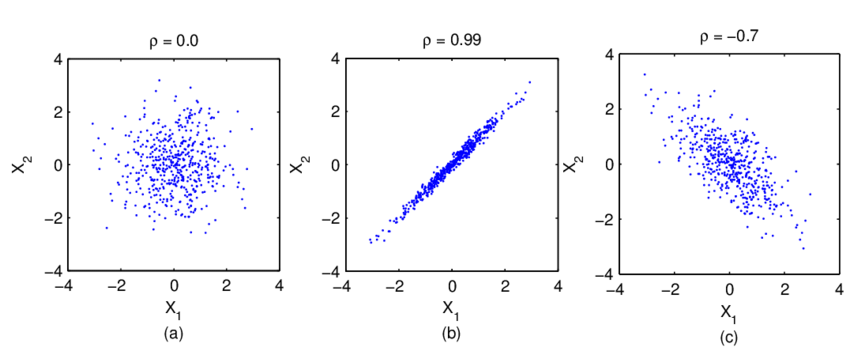
- (a)의 그림같은 경우 산점도를보면 다양하게 퍼져있기 때문에 상관계수 = 0의 값을 가지고
- (b)의 경우 우상향의 직선에 가까운 산점도를 가지기 때문에 양의 상관관계를 가지며 상관계수 = 1이다.
- (c)의 경우조금 퍼져있기는 하지만 음의 상관관계의 성질을 가지기 때문에 상관계수 = -0.7 이다.

- 위 그림 처럼 산점도가 나오게 된다면 상관계수는 직선의 관계를 가지지 않기때문에 모두 상관계수 = 0이다.
상관계수 공식(피어슨 상관계수)
상관계수 공식
$$ p = \frac{Cov(X_1,X_2)}{\sigma(X_1) * \sigma(X_2)}$$
- Cov(x,y)는 x,y의 공분산
- $ \sigma(x) $는 x의 표준편차
공분산
분산은 한 변수가 평균에 대해 얼마나 떨어져있나(거리) 편차제곱의 합의 평균 이지만, 공분산은 두 변수에서 각각 평균에 얼마나 떨어져 있는지를 수치화 한것
$$ Cov(x,y) = \sum{(x_i값-x평균) * (y_i값-y평균)} / 데이터 수 $$
예를들어, X의 데이터 = [5, 10, 9, 8, 7], Y의 데이터 = [8, 6, 1, 3, 5]
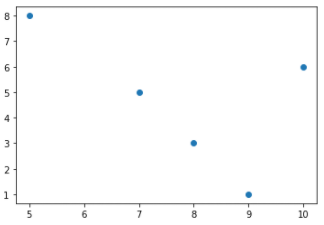
x평균 = 7.8, y평균 = 4.6
Cov(x,y) = (5 - 7.8)(8 - 4.6) + (10 - 7.8)(6 - 4.6) + (9 - 7.8)(1 - 4.6) + (8 - 7.8)(3 - 4.6) + (7 - 7.8)(5 - 4.6) / 5
Cov(x,y) =-2.28
공분산 수치의 의미
- Cov(x,y) > 0 x값 증가시 y값 증가
- Cov(x,y) < 0 x값 증가시 y값 감소
- Cov(x,y) = 0 x와y가 선형적인 관계가 없음
표준편차
$$ 표준편차 = \sqrt{분산} $$
$$ 표준편차(x) = \sqrt{\sum{(x_i값-x평균)^2} / 데이터 수} $$
표준편차는 분산의 제곱근을 한 값이고, 데이터들이 평균에서 얼마나 떨어져있는지를 나타내는 수치이다.
예를들어, x의 평균이 100이고, 표준편차값이 10이면 x의 데이터들의 값이 90 ~ 110 사이에 있다는 것을 알 수 있다.
상관계수
공분산값은 범위가 정해져 있지않아서, 공분산 값의 정규화를 통해 -1 ~ 1의 범위에서만 나오게 하는 것이 상관계수.
- p > 0 (-1 <= 0 <= 1) 일때 : 양의상관관계, 한 특징 값이 커지면 다른 특징 값도 커진다.
- p < 0 (-1 <= 0 <= 1) 일때 : 음의상관관계, 한 특징 값이 커지면 다른 특징 값은 작아진다.
- p = 1 : 모든 점들이 우상향 직선의 기울기의 값위에 위치한다. (데이터들 완전한 직선의 형태라는 것)
- p = -1 : 모든 점들이 우하양 직선의 기울기의 값위에 위치한다.
- p = 0 : 상관관계가 거의 없다는 것을 의미
※ 보통 p값이 ±0.3 정도면은 약한 상관관계를 의미하고, ±0.7정도면 강한 상관관계를 의미한다.
import matplotlib.pyplot as plt
import numpy as np
import math
import scipy as sp
x = [5, 10, 9, 8, 7]
y = [8, 6, 1, 3, 5]
N = len(x)
x_m = np.mean(x)
y_m = np.mean(y)
# 데이터의 편차
x1 = x - x_m
y1 = y - y_m
#편차제곱을 통해 마이너스 제거
xx1 = x1 * x1
#std_x은 x의 표준편차
std_x = np.sqrt(np.sum(xx1) / N)
print("x표준편차 : ", std_x)
# Y도 똑같이 진행
yy1 = y1 * y1
std_y = np.sqrt(np.sum(yy1) / N)
print("y표준편차 : ",std_y)
#xy의 공분산
xy = x1 * y1
cov_xy = np.sum(xy)
print("Cov(x,y) : ", xy_sum / N)
print((cov_xy / N) / (std_x * std_y))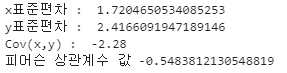
'머신러닝 > 머신러닝 수학' 카테고리의 다른 글
| 시그모이드 함수 미분법 Sigmoid Differential 정리 - [머신러닝] (0) | 2021.06.02 |
|---|
