<선형회귀(Linear Regression)>
선형회귀 머신러닝을 공부하며 선형회귀를 다들 귀에익을 정도로 들었을 것이다.
그래서 선형회귀가 무엇인가?
선형회귀는 변수들 간의 함수관계를 분석하는 방법으로, 독립변수가 종속변수에 미치는 영향력의 크기를 파악하고, 이를 통해 독립변수의 일정한 값에 대응하는 종속변수 값을 예측하는 모형을 산출하는 방법
자 저런 말들은 머리로 이해하는데 직관적으로 와닫지 않는다. 우리는 어려운 말에는 예제를 들어가며 쉬운 길을 찾는다.
그래서 선형회귀를 쉽게이해 하기위해 예를 들어보면은 년도수를 X에 두고, 강남 아파트 가격 데이터를 Y라고 한다.
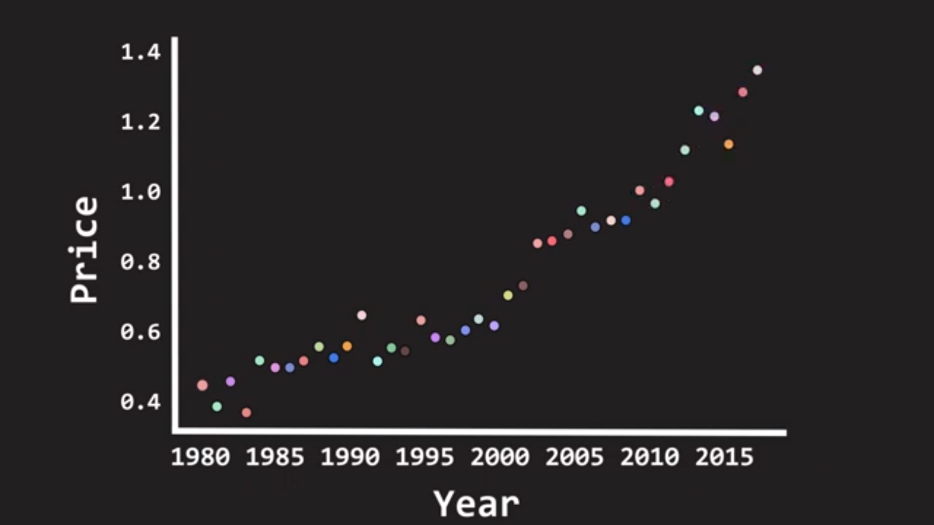
Year과 강남아파트 Price의 데이터 점들을 통해서 두 변수의 관계를 가장 잘 나타내줄 수 있는 최적의 직선을 긋는다.
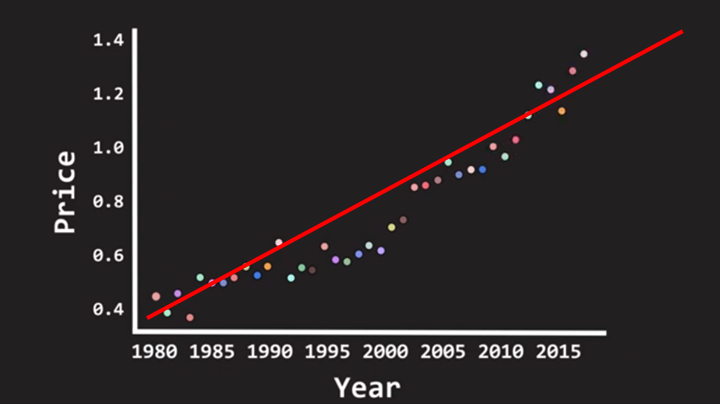
직선의 방정식 $ Y = aX+b $ X에 Year대입함으로 X년도의 강남 아파트 가격을 예측 할 수 있다.
그래서! 그 직선의 방정식 $ ax + b $의 기울기 a와 Y절편 b는 어떻게 구하는지를 알아보자.
최소 제곱법(Ordinary Least Squares)
최소제곱법은 실제 값과 직선의 값에 차이가 최소가 되는 해를 구하는 방법이다.
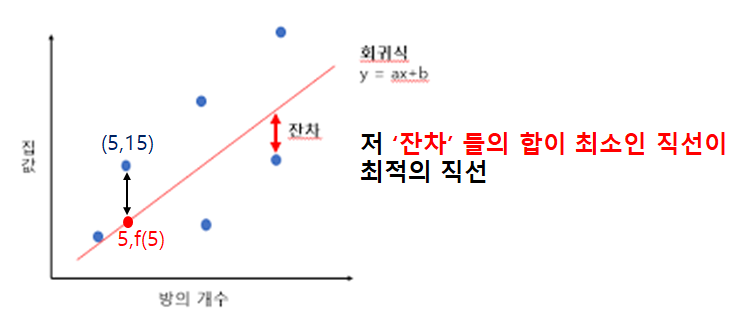
최대한 쉽게말해, 아래 그림의 데이터 점들의 Y값과 $ Y = aX+b $ 직선에서 Y값의 차(잔차)들의 제곱의 합이 최소가 되는 직선을 그리는 것을 말한다.
※ 여기서 잔차들을 제곱하는 이유는, 데이터들이 직선의 위아래로 분포 될 수 있기 때문에 잔차의 ±값을 제곱을하여 모두 +로 바꾸기 위함이다.
$$ \sum_{i=1}^{n} (y_i - (aX_i+b))^2$$
- $ y_i $는 데이터 y의 값
- $ (aX_i + b) $는 직선의 방정식, 총 i개의 데이터들의 X값들을 넣어 잔차를 구함
기울기 a값 과 Y절편 b값을 구하는 공식
$$ b = Y의평균 - (a * X의평균) $$
$$ a = \frac{\sum_{i=1}^{n}(X-X의평균)*(Y-Y의평균)}{\sum_{i=1}^{n}(X-X의평균)^2} $$
※ a와 b의 값에 대한 증명은 아래에 달아놓겠습니다.
선형회귀 실습
데이터 200명의 키, 몸무게 데이터

산점도 확인
df = pd.read_csv("hw_200.csv")
# 해당 컬럼 삭제
df = df.drop(["Index"], axis = 1)
df.sample(5)
X = df["Height(inches)"]
Y = df["Weight(pounds)"]
plt.plot(X,Y, 'go')
line_filtter = LinearRegression()
line_filtter.fit(X.values.reshape(-1,1), Y)
# 원하는 X값을 넣어 Y(무게를)를 예측 할 수 있다. 70인치의 키를 가진 사람의 몸무게예측
print(line_filtter.predict([[70]]))
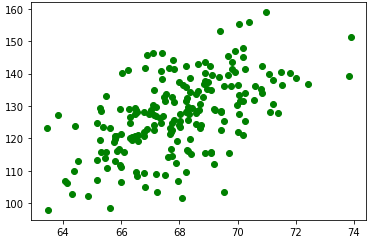
학습후 선형 직선 그리기
#Kg, Cm로 변환해서 선형변환
Cm_X = X * 2.54
Kg_Y = Y * 0.453592
line_filtter = LinearRegression()
line_filtter.fit(Cm_X.values.reshape(-1,1), Kg_Y)
plt.plot(Cm_X, Kg_Y, 'go')
plt.plot(Cm_X,line_filtter.predict(Cm_X.values.reshape(-1,1)))
plt.show()
print(line_filtter.predict([[178]]), "kg")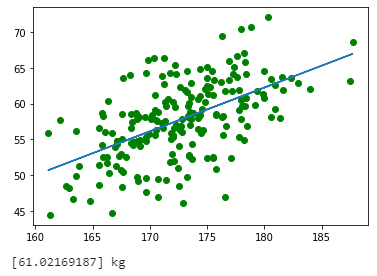
편미분을 이용한 최소제곱법 [기울기 a, Y절편 b] 공식 유도
a값과 b값이 어떻게 나오는지 궁금해서 증명식 한번 적어봤습니다.
궁금하신 분만 보시는 것을 권장드립니다.
1) $ \sum_{i=1}^{n} (y_i - (aX_i+b))^2$ 에서 b값에 편미분 진행해, b값 유도

2) $ \sum_{i=1}^{n} (y_i - (aX_i+b))^2$ 에서 a값에 편미분 진행해, a값 유도
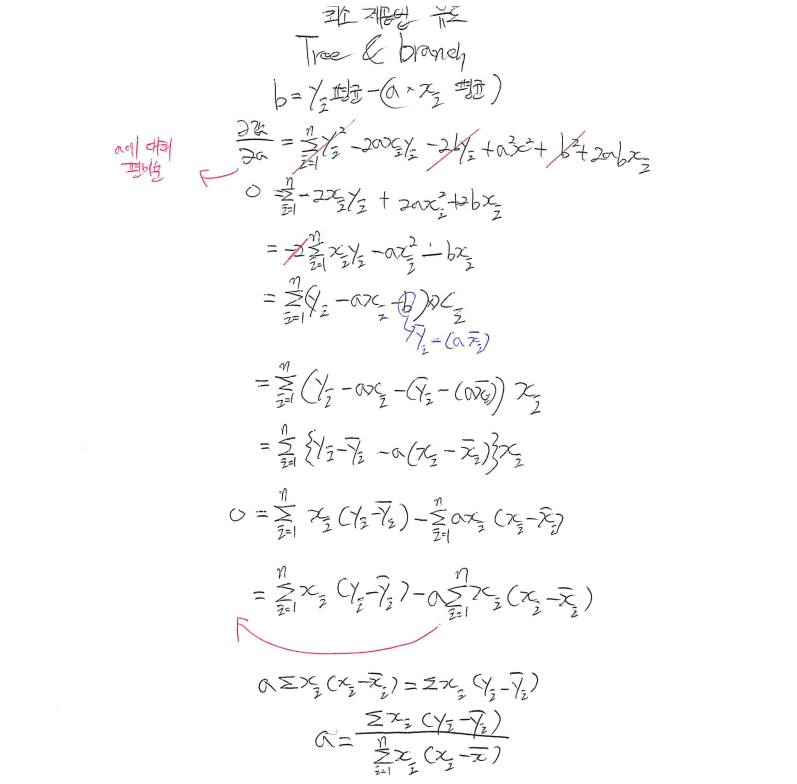
3) $ a = \frac{\sum_{i=1}^{n}(X-X의평균)*(Y-Y의평균)}{\sum_{i=1}^{n}(X-X의평균)^2} $분모, 분자 증명

'머신러닝 > 머신러닝 알고리즘' 카테고리의 다른 글
<선형회귀(Linear Regression)>
선형회귀 머신러닝을 공부하며 선형회귀를 다들 귀에익을 정도로 들었을 것이다.
그래서 선형회귀가 무엇인가?
선형회귀는 변수들 간의 함수관계를 분석하는 방법으로, 독립변수가 종속변수에 미치는 영향력의 크기를 파악하고, 이를 통해 독립변수의 일정한 값에 대응하는 종속변수 값을 예측하는 모형을 산출하는 방법
자 저런 말들은 머리로 이해하는데 직관적으로 와닫지 않는다. 우리는 어려운 말에는 예제를 들어가며 쉬운 길을 찾는다.
그래서 선형회귀를 쉽게이해 하기위해 예를 들어보면은 년도수를 X에 두고, 강남 아파트 가격 데이터를 Y라고 한다.

Year과 강남아파트 Price의 데이터 점들을 통해서 두 변수의 관계를 가장 잘 나타내줄 수 있는 최적의 직선을 긋는다.

직선의 방정식 $ Y = aX+b $ X에 Year대입함으로 X년도의 강남 아파트 가격을 예측 할 수 있다.
그래서! 그 직선의 방정식 $ ax + b $의 기울기 a와 Y절편 b는 어떻게 구하는지를 알아보자.
최소 제곱법(Ordinary Least Squares)
최소제곱법은 실제 값과 직선의 값에 차이가 최소가 되는 해를 구하는 방법이다.
최대한 쉽게말해, 아래 그림의 데이터 점들의 Y값과 $ Y = aX+b $ 직선에서 Y값의 차(잔차)들의 제곱의 합이 최소가 되는 직선을 그리는 것을 말한다.
※ 여기서 잔차들을 제곱하는 이유는, 데이터들이 직선의 위아래로 분포 될 수 있기 때문에 잔차의 ±값을 제곱을하여 모두 +로 바꾸기 위함이다.

$$ \sum_{i=1}^{n} (y_i - (aX_i+b))^2$$
- $ y_i $는 데이터 y의 값
- $ (aX_i + b) $는 직선의 방정식, 총 i개의 데이터들의 X값들을 넣어 잔차를 구함
기울기 a값 과 Y절편 b값을 구하는 공식
$$ b = Y의평균 - (a * X의평균) $$
$$ a = \frac{\sum_{i=1}^{n}(X-X의평균)*(Y-Y의평균)}{\sum_{i=1}^{n}(X-X의평균)^2} $$
※ a와 b의 값에 대한 증명은 아래에 달아놓겠습니다.
선형회귀 실습
데이터 200명의 키, 몸무게 데이터

산점도 확인
df = pd.read_csv("hw_200.csv")
# 해당 컬럼 삭제
df = df.drop(["Index"], axis = 1)
df.sample(5)
X = df["Height(inches)"]
Y = df["Weight(pounds)"]
plt.plot(X,Y, 'go')
line_filtter = LinearRegression()
line_filtter.fit(X.values.reshape(-1,1), Y)
# 원하는 X값을 넣어 Y(무게를)를 예측 할 수 있다. 70인치의 키를 가진 사람의 몸무게예측
print(line_filtter.predict([[70]]))

학습후 선형 직선 그리기
#Kg, Cm로 변환해서 선형변환
Cm_X = X * 2.54
Kg_Y = Y * 0.453592
line_filtter = LinearRegression()
line_filtter.fit(Cm_X.values.reshape(-1,1), Kg_Y)
plt.plot(Cm_X, Kg_Y, 'go')
plt.plot(Cm_X,line_filtter.predict(Cm_X.values.reshape(-1,1)))
plt.show()
print(line_filtter.predict([[178]]), "kg")
편미분을 이용한 최소제곱법 [기울기 a, Y절편 b] 공식 유도
a값과 b값이 어떻게 나오는지 궁금해서 증명식 한번 적어봤습니다.
궁금하신 분만 보시는 것을 권장드립니다.
1) $ \sum_{i=1}^{n} (y_i - (aX_i+b))^2$ 에서 b값에 편미분 진행해, b값 유도

2) $ \sum_{i=1}^{n} (y_i - (aX_i+b))^2$ 에서 a값에 편미분 진행해, a값 유도
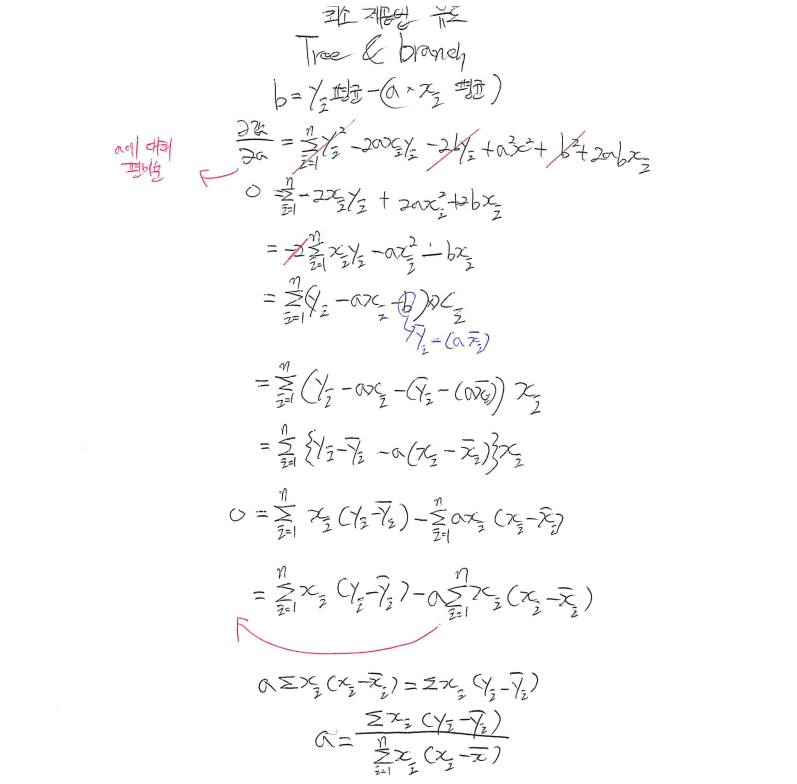
3) $ a = \frac{\sum_{i=1}^{n}(X-X의평균)*(Y-Y의평균)}{\sum_{i=1}^{n}(X-X의평균)^2} $분모, 분자 증명

