심층 신경망 과 최적화
- 딥러닝 학습의 문제점화 해결방법
- 기울기 소실(Gradient Vanishing)
- 가중치 초기화
- 최적화 알고
기울기 소실(Gradient Vanishing)
더 깊은 Layer 에서는 더 학습이 잘되는거 아닌가? 하지만 기울기 소실이 발생한다.
기울기 소실이란? : Out에 나오는 값과 멀이질 수록 학습이 모호하게 진행됨 Sigmoid함수 에서의 1보다 작으면 0에 가까워진다는 이유로 계속 0에 가까워져 기울기가 모호해짐(역전파시 0에 수렴하는게 많음)
- Sigmoid 도함수의 최대값은 0.25
- ReLU 도함수 값이 0이나 1이기 때문에 컴퓨터 측면에서 경제적 학습도 빠름
- Leaky ReLU 0보다 작은 경우 ReLU에서 신경이 죽어버리는 현상 극복
- Tanh 함수값의 범위가(-1,1), 도함수의 최댓값 1
가중치 초기화
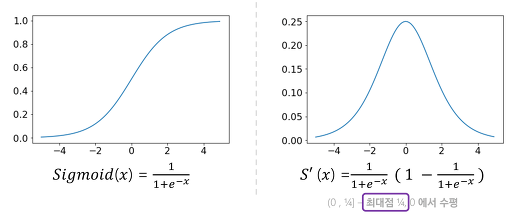
- t = wx + b 에서 시그모이드 함수 미분시 t가 5만 넘어도 0에 수렴 -> 기울기 소실 문제 발생
- 가중치w를 0으로 초기화하면 두번째 층 레이어 의 뉴런이 모두 같은 값이 전달됨

표준편차를 0.01로 하는 정규분포 형태로 초기화 했을 때 0.5 중심으로 모여있음.
- Xavier initalization (RBM보다 좋은 방법이 생김) 하나의 노드에 몇개의 입력이고 몇개의 출력인가에 맞게 비례해 초기값을 주는 방법.
- 표준 정규 분포를 입력 개수의 제곤근으로 나누어줌.
- W = np.random.randn(n_input,n_output)/sqrt(n_input)


- He initalization ReLU 함수에 맞는 초기화 법
- input 갯수의 절반의 제곱근으로 나누어 주면 된다.
- W = np.random.randn(n_input,n_output)/sqrt(n_input/2)
[딥러닝] 뉴럴 네트워크 Part. 6 - 가중치 초기화
이전 까지의 내용 이전 글에서는 Vanishing Gradient 현상이 왜 일어나는지, 어떻게 해결해 나가는지와 가중치 초기화 (weight initialization) 가 왜 중요한지에 대해 살펴보았습니다. 이번 글에서는 가중
gomguard.tistory.com
최적화(Optimization) 알고리즘
- SGD
- 손실함수를 계산할 때 전체 Traing set을 사용함
- 계산량이 너무 많아 지는것을 방지
- 전체 데이터에서 일부 데이터의 모음에 대해서만 loss function을 계산
- data를 sampling해서 gradient descent를 진행한다. 이를 반복
loss function 재정리
신경망을 학습할 때 학습 상태에 대해 측청하는 하나의 지표로 사용. 신경망의 가중치 매개변수들이 스스로 특징을 찾아 가기에 이 가중치 값이 최적이 될 수록 해야 하며 잘 찾아가고 있는지 볼때 손실함수를 본다.
- Mean Squared Error(평균제곱오차)
- 예측 값과 실제 값의 차이를 제곱하여 평균을 낸것
- 예측값과 실제값의 차이가 클 수록 평균 오차제곱도 커짐(작아야 좋음)𝐸=1𝑛∑𝑘𝑛(𝑦𝑘−𝑡𝑘)2E=1n∑kn(yk−tk)2
- Cross entropy error
- 기본적으로 분류 문제에서 one hot 코딩을 했을 경우에만 사용할 수 있는 오차 계산 법 밑이 자연로그인 e를 예측값에 씌워서 실제 값과 곱한후 전체 값을 합한후 음수로 변환
- 엔트로피가 낮을 수록 좋다𝐸=−∑𝑘𝑡𝑘log𝑦𝑘E=−∑ktklogyk
알고리즘 정리 사이트
Gradient Descent Optimization Algorithms 정리
Neural network의 weight을 조절하는 과정에는 보통 ‘Gradient Descent’ 라는 방법을 사용한다. 이는 네트워크의 parameter들을 $\theta$라고 했을 때, 네트워크에서 내놓는 결과값과 실제 결과값 사이의 차이
shuuki4.github.io
'공부 > AI School 인공지능 여름캠프' 카테고리의 다른 글
| 딥러닝 CNN(Convolution Neural Network) 합성곱신경망 - [AI School] (0) | 2021.05.04 |
|---|---|
| 딥러닝 데이터 변형, 과대적합(Overfitting) & 과소적합(Underfitting), Dropout - [AI School] (0) | 2021.05.04 |
| 딥러닝 ANN(Artificial Neural Network), 손실함수, 역전파법 (0) | 2021.05.03 |
| 딥러닝 텐서플로우 소개 및 기본 사용법 - [AI School] (0) | 2021.05.03 |
| 딥러닝 시작, 신경망 기초 - [AI School] (0) | 2021.05.03 |
